O trabalho prático, no qual se está executando a tarefa e sobretudo de modo investigativo, buscando encontrar respostas, certamente é um dos métodos mais didáticos para o auto-aprendizado e para o desenvolvimento do músculo.
Imagina a cena em que um homem iletrado adquire o trabalho de construir uma pequena torre usando apenas bambu e sisal (uma pioneiria interessante, certamente) e então ele inicia o seu trabalho. Certamente a primeira vez será incrível em níveis de tentativas e erros, análises. Coloca uma coisa ali e vê se dá certo ou não, ou o que acontece. E com o tempo todas aquelas informações são registradas na memória, um senso crítico se desenvolve sobre a questão. E certamente, depois de muitas tentativas ele consegue fazer uma pequena torre simples.
Bem, então é dado uma segunda construção para ele fazer. Uma torre de bambu, mas que deve conter pelo menos 5m de altura e em seu topo uma plataforma que consiga sustentar o peso de duas pessoas. Então dessa vez será um quebra-cabeça para o construtor. Talvez uma altura maior que a anterior, e nisso perceberá que as suas amarras não eram firmes o suficientes e nisso ele pode buscar tentar desenvolver uma modo mais firme de fazer as amarras, ou então ir “buscar” o conhecimento que já existe sobre amarras, e então pode adquiri-lo, treiná-lo e apreender através da prática. Também desenvolverá modos para subir na torre. E certamente fará testes e buscará modos para se construir tal plataforma que atenda as condições.
Após esse trabalho recebe mais uma: Uma torre de 7m com uma polia que suporta até 100 kg de carga e além disso, fazer um “projeto”, isso é: estimar a quantidade de bambus que será usado, quantidade de cordas, material, a forma da torre e o tempo. Isso certamente é muito mais difícil, algo inteiramente inédito. Para começar iria buscar entender o que é uma polia, como funciona, as regras funcionais, e construiria um modelo em tamanho real ou escalar numa pequena altura para testar. Certamente iria tentar fazer algo em escala, desenhar algo, buscar “precisões”; moldes, desenhos; nisso, iria acabar desenvolvendo um pouco de matemática ou apreendo-a, principalmente uma regra de três, multiplicações, divisões; contudo, difícil imaginar que iria pensar em Geometria Analítica, vetores, tensão, integrais de linhas, derivadas parciais, momento angular, centro de massa. Mas com muito esforço iria conseguir fazer um modelo e construir.
Bem, precisamos usar tal método para aprender muitas coisas. Em especial para com a matemática. Infelizmente, em geral, hoje o sistema se prende ao teórico, as regras de sintaxe, gramaticais, algorítmicas; mas não buscando levar e mesclar tal com o desenvolvimento prático e intelectual, em nível de produzir um senso crítico, analítico, dedutivo e lógico. Os músculos responsáveis pelo exercício da matemática ficam atrofiados, não se desenvolvem. E claro, que uma pessoa que nunca fez flexão na vida, aos 16 anos não irá achar nada divertido fazer 30 flexões.
Uma sugestão que dou aos pais, educadores, professores e para a mente pensante em geral, aquele que busca desenvolver a matemática. É brincar de “construir torres” com a matemática visando trabalhar com os músculos do raciocínio dedutivo e lógico. E consequentemente, com isso, desenvolver também a parte gramatical, algorítmica e sintática da linguagem matemática.
Exercícios de lógica é uma boa. Xadrez não, pois é algo avançado, e a pessoa teria que estudar bem a coisa, para não apenas jogar, mas jogar de forma estratégica. Sodoku, puzzles entre tantos outros. Mandar projetar e construir algo simples e depois coisas mais sofisticadas. Que tal projetar uma mesa para o seu quarto? Buscar medir a quatidade usada de água num minuto no banho, de modo a formar uma tabela indicando o tempo de uso e a quantidade. Construir uma balança para medir coisas até 10kg, com precisão de 50g. Basta começar imaginar situações no dia-dia que ao invés de “sedentarizar” a coisa, poderia usá-la para o aprendizado e desenvolvimento físico e mental do individuo.
E aqui vão algumas sugestões em vários níveis de coisas interessantes e algo para desenvolver esse raciocínio, em que uma pessoa de nível de segundo grau certamente teria capacidade para conseguir alcançar tais objetivos.
1. Montar uma função data, f(x), em que x = número de dias. De modo que por resultado se saiba o ano, mês, dia do mês, e dia da semana, de forma precisa. Por exemplo: Hoje é dia 28, quinta-feira, de agosto de 2008, daqui 265 dias quando seria?
2. Pegar o algoritmo da multiplicação e da divisão e desenvolvê-lo. Como se chega em tal? Por que funciona?
3. Medir o tamanho das árvores e postes na sua rua, sem subir nelas.
4. Descobrir as velocidades confortáveis e máximas para cada marcha numa bicicleta.
5. Qual a probabilidade da Mega-sena e fazer comparações de modo a equivaler vários tipos de jogadas e combinações com dados.
6. Descobrir o que é mais pesado entre terra, areia, cimento, barro, e vários farelos; quantificar a densidades de tais na água.
7. Descobrir qual é as medidas e razões que há entre os intervalos das notas no braço do violão.
8. Contar o número de passageiros num ônibus ou vão, marcar os pontos de saída de tais. E depois buscar quantificar a distância que tal transporte poupou para eles, e num geral, e de tempo, fazer médias, com número de pessoas e de ônibus semelhantes. E nisso buscar compreender um pouco de senso da logística de transporte.
9. (para alguém que não aprendeu Progressão Aritmética) Dar-lhe a tarefa de contar uma soma de [1, 1000]. Do tipo: “1 + 2 +3 +4 + 5 + ... + 1000 = ?” E desafiá-lo a tentar encontrar um padrão nessa soma e assim desenvolver uma forma de encontrar esse resultado com poucas contas.
10. Tomar por base o tamanho de alguns tijolos e estipular a quantidade que deve ter sido usado para construir as paredes da sua casa.
11. Construir uma pequena catapulta balística de modo a conseguir lançar fubécas e pequenos objetos. Buscar tentar quantificar esses lançamentos, e entender a mecânica da coisa. E depois tentar construir um outro aprimorado na mesma escala, mas conseguindo lançar o objeto mais longe. E colocar marcadores de modo que consiga prever onde que é o objeto cairá.
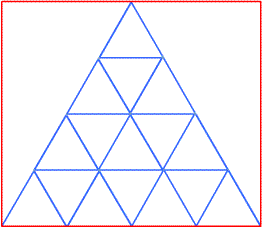
12. Formular uma equação para descobrir o número de triângulos contidos num triângulo maior, em função do número de triângulos na base, de modo que todos sejam eqüiláteros. (ver a figura tema) E buscar variações, como quantos de ponta para cima, de ponta para baixo? Quantos conteria em cada andar? Qual seria o perímetro total para todos os triângulos de lado 1? Etc. (esse é muito bom)
13. Pegar gravetos de vários espécimes de árvores e tentar quantificar (talvez com indicadores e escalas próprias) o índice de resistência de cada um para peso, envergadura, torção, corte; qual o seu peso, flutuabilidade, durabilidade até começar a apodrecer...
14. Construir um relógio solar. Um relógio do tipo ampulheta. E escalar as horas, ou minutos, segundos.
15. Tentar encontrar algum padrão entre os números primos de forma a poder prevê-los. (esse é um dos grandes problemas da matemática, e certamente, se você conseguir, receberá milhões ($) ).
16. Descobrir a matemática nas notas musicais e escalas, como funciona um afinador. E desenvolver um instrumento com todas as notas, afinadas, pelo menos uma oitava. Sugestão: copos com água, barras de metal (tipo um xilofone).
17. Encontrar uma forma, visando a logística, para organizar os móveis da casa, de modo a possuir maior espaço útil, praticidade e vizualização.
18. Buscar construir formas variadas de um castelo de cartas de baralho e classificar a resistência de cada um, quanto a suportar peso, vento e vibração.
Também pode-se aproveitar algumas aptidões já desenvolvidas e buscar nelas dados e informações lógicos, que até mesmo pode ajudá-la. Por exemplo:
1. Numa cobrança de penalty num futebol de salão ou campo, medir quais os locais em que o goleiro teria mais dificuldade para pegar a bola numa velocidade x, e quanto tempo ele levaria para conseguir chegar em tal ponto para realizar uma defesa; então se fosse cobrar em tal lugar, qual deveria ser a velocidade do chute, para ser indefensável?
2. Numa partida de cinuca, qual as direções que as bolas tomam quando são acertadas em determinadas regiões, ângulos e trajetórias? Como se comporta a trajetória da bola quando se faz tabelas com a borda da mesa? De modo a ficar previsível os lances.
3. Qual a melhor forma de se chutar visando adquirir maior velocidade na bola. (Buscando quantificar as diferenças).
4. Num jogo de truco, para 2, 4 ou 6 pessoas. Qual a probabilidade de você vencer, de alguém ter uma carta melhor, um 3, ou 2, ou uma manilha. Na primeira rodada, segunda e terceira. (há livros que já possuem tais informações, mas o importante é a pessoa desenvolver e construir esses valores)
5. Fazer relações quantificando o nível de esforço, e marchas e velocidades confortáveis para se pedalar em regiões de diversas inclinações. E buscar fazer uma trajetória, e planejá-lo, de modo a se chegar no final com o melhor tempo e mínimo cansado possível.
6. Identificar quais são os locais – pelo menos no chão – mais propensos a se quebrar, desgastar. Onde há maior trafego de pessoas, pesos, objetos pesados, arrastados. Quantificar isso. E buscar medidas, mudanças, para evitar tais desgastes, buscando moderar e suavizar todo o sistema.
7. Desenhar estruturas, objetos tridimensionais no papel. Buscando preservar a perspectiva, projeção, simetria, proporção e medidas. (buscar objetos cada vez mais complexos).
Os professores de matemática podem desenvolver outros modelos e usá-los como trabalhos especiais, em grupo e individuais. De modo a desenvolver tais áreas. E uma melhores coisas do trabalho prático, dessas experiências. É que o trabalho o ocupa, faz a mente trabalhar, gostar da coisa, e no final, quando é concluído há a “realização”, a conclusão. E não meramente a nota de uma prova teórica dos conteúdos teóricos gramaticais e sintáticos expostos em sala de aula ou no livro didático.
Em geral, muitos professores olham as notas dos alunos, fazendo médias do tipo: “sou um bom professor, alguns ou vários alunos tiveram um bom desempenho na prova”. Ou mesmo outorgando ao aluno como a total responsabilidade: “Esse aluno tem dificuldade, não consegue aprender.” Quando na verdade, deveriam ver como cada nota de cada aluno, como sendo a nota, a avaliação para com o professor. Mostrando a capacidade de tal em ter ensinado o aluno, ou mesmo de motivá-los. E uma das coisas tristes é essa forma de avaliação usada hoje, que é “fácil” – escolho alguns exercícios, imprimo, tiro xérox e cada e vamos medir o desempenho de cada um – para o professor. Mas até aonde isso avalia? Serve para todos os casos, todos os alunos? Não é um modelo construtivo.
Usando de experiências bem elaboradas, planejadas e orientadas. O aluno é grandemente motivado; e desenvolverá muito além do que uma típica “aula” de hoje: com a lousa, o giz, os números, os títulos, as fórmulas, os exemplos, as lições de casas e provas. E por fim, será muito mais claro de se avaliar o grau de desenvolvimento do aluno, e até mesmo identificar as debilidades.
Sempre uso exercícios de lógica e de dedução com os alunos particulares. E sempre tento avaliar de inicio as áreas de debilidade dele. E por incrível que pareça, a menor parte é quanto a matemática formal, as regras gramaticais, sintáticas e fórmulas. Mas na maioria das vezes, mesmo quando há debilidades dessas, a causa é: atrofia dos músculos do/a: raciocínio, lógica, dedução, criatividade, abstração, motivação, construção do pensamento, critica, observação e análise, concentração e intuição.
E boa parte dessas deficiências não se trabalhar com exercícios de regra de três com o exemplo do Zecá que foi comprar pão na padaria. Ou com aqueles vários: “Agora calcule...; simplifique”. Muito menos que são poucos os alunos que conseguem interagir com esse tipo de exercício.
Sinceramente, apenas tive um único aluno, que tinha todas essas áreas desenvolvidas, mas que a debilidade estava quando a linguagem matemática, a escrita, a gramática, sintaxe. É aquela coisa, ele entende bem, consegue desenvolver e racionar mentalmente, perfeito, mas o problema está na hora de passar pro papel de modo que o professor verifique se ele acertou, se escreveu bonito. E quando era apenas esse o problema, foi fácil de se resolver; com 1 mês de aula, duas por semanas, apenas explicando e treinando a matemática formal; e ele pegou e ficou bom na coisa.
É aquela coisa, o menino não tem vontade de comer. Aí os pais dão vários remédios, tônico, e a criança continua não comendo. Se virão para fazer comidas atrativas e deliciosas, mas o menino não come. E começa a julgar a criança, falar até mesmo mal de tal, como qualificando que a nota dele está “vermelha”. E enquanto isso ela vai gostar de comer? Não. Até que resolvem levar no especialista, e é feito um diagnóstica e percebe que tal está com alguma doença, ou falta de algum nutriente especifico, ou uma infecção; aí trata-se daquilo. E logo a criança passa a comer normalmente e a gostar de comida. E então a pergunta vem: “Por que em geral as pessoas não gostam (não querem) comer matemática?”
Contudo, o paradigma continua: “Por que o professor terá tanto trabalho assim, se o que o MEC exige é apenas o conteúdo; e em troca são mal recompensados com salários baixíssimos para uma atividade tão digna, senão a mais digna de todas.”