Há muitos objetos nos quais não são possíveis calcular seu volume exato, ou mesmo área, usando de métodos simples, como “Base x Altura”; porque há “curvas”, “deformações”, inclinações, entre outros, de modo, que o mais próximo seria aproximar de modo “ad infinitum” do seu volume exato.Com a evolução da matemática, especialmente com Isaac Newton, o qual consolidou melhor o Cálculo Diferencial e Integral, hoje, podemos encontrar precisamente a área e volumes de tais objetos, usando-se da Função Integrante.
O Cilindro Reto
 Temos uma circunferência simples, assumindo o papel de “base” do objeto. Olhando por um ponto de vista perpendicular/ortogonal ao plano no qual pertence essa circunferência, temos essa visão.
Temos uma circunferência simples, assumindo o papel de “base” do objeto. Olhando por um ponto de vista perpendicular/ortogonal ao plano no qual pertence essa circunferência, temos essa visão.Para calcular a área dessa figura, no caso um circulo, usamos A = π.r²

Fazer uma “extrusão” de tal base até uma altura H, teremos então um cilindro. Seria como pegar uma carta de baralho (base), e então colocar várias uma em cima da outra, de forma a manter a mesma forma, até uma altura H.
Para calcular o volume desse objeto, um cilindro, basta multiplicarmos a área da base pela altura: V = Abase x H
Para calcular o volume desse objeto, um cilindro, basta multiplicarmos a área da base pela altura: V = Abase x H
O mesmo para um livro, pegue a área da base, ou seja, de uma folha, e multiplique pela altura formada, no caso a espessura do livro – o número de páginas vezes a espessura da folha.
O mesmo ocorre no caso abaixo, sendo a base um quadrado.
Então, não importa qual seja o formato da base, o volume, será sempre a área da base vezes a altura do sólido. Há os outros objetos, como esferas, cônicas entre outras que o mesmo não vale; estamos tratando do caso cilíndrico – Princípio da Extrusão. Nos demais casos, a formato da base varia conforme a altura, ou seja, a área não é fixa mas é uma função variável. Veremos a seguir, que mesmo para tais, podemos calcular o volume do mesmo modo, Abase x Altura, só que a Abase = f(x), e a altura.
Sólido de Revolução
Para uma f(x), em R.
Podemos fazer um sólido de revolução, que seria girar tal imagem, em torno de um eixo qualquer. No caso, giraremos em torno do eixo x:

Pode-se reparar, que qualquer plano perpendicular ao eixo x, a sua intersecção com o gráfico (a figura, sólido) formado, será algo circular. Pois, na revolução, o que se faz é pegar um ponto f(x) e girar (360º ou 2 ) em torno de um centro, no caso, x. Com isso, se tem uma circunferência.

 Como se pode ver. Analisando a intersecção do plano possuí um formato de um círculo. Mas num caso genérico. Supondo que não sabemos que o formato é um círculo, simplesmente podemos dizer, que a figura formada tem uma área, A(x).
Como se pode ver. Analisando a intersecção do plano possuí um formato de um círculo. Mas num caso genérico. Supondo que não sabemos que o formato é um círculo, simplesmente podemos dizer, que a figura formada tem uma área, A(x).Para saber o volume de tal sólido. Basta somarmos todas as áreas da base – os círculos – pela altura – de a até b, ou seja: H = b – a .
Como vimos anteriormente, para calcular o volume, temos que pegar área da base, A(x), e multiplicar pela altura. Agora, a situação é que a base é uma função f(x). Então, “A(xi ). ”é o mesmo que a “A(x).H” (área da base x altura). E nisso teremos o volume de cada um desses minúsculos segmentos. Então, o volume total, seria a soma de todos os volumes desses segmentos:

Isso é “A Soma de Riman.”
Para incluir os segmentos, de modo “ad infinitum”, pois há infinitos "xi" dentro de Δx. Para isso, fazemos o limite da soma de Himan, quando o tamanho da partição (ρ) tender a zero. O que resulta na Integral.
Para incluir os segmentos, de modo “ad infinitum”, pois há infinitos "xi" dentro de Δx. Para isso, fazemos o limite da soma de Himan, quando o tamanho da partição (ρ) tender a zero. O que resulta na Integral.

>>> Esse é denominado como “Método das Fatias”, para encontrar volume.
Nos casos de Revolução, a área das fatias, será a área de um circulo. No qual o raio é a imagem, f(x), em x. O que você pode facilmente verificar. Com isso, A(x) = π.f(x)². Então, o volume de sólidos de revolução, pode-se escrever como:
 Exemplo:
Exemplo:A função: f(x) = √x , no intervalo [0, b]

Fazendo a revolução desse gráfico, em torno do eixo x, obtemos:

(fatiando...)
No qual o raio é a própria imagem de x, ou seja, f(x)= √x. Então, a área dessa circunferência é de π.(√x)² = π.x
Então, o volume do sólido, no intervalo [0, b], supondo que b = 1, é:
 Agora, caso queira calcular a área dessa superfície. Ao invés de procurar saber a área dos círculos formados pelas fatias, calcule a borda, ou o comprimento da circunferência e integre.
Agora, caso queira calcular a área dessa superfície. Ao invés de procurar saber a área dos círculos formados pelas fatias, calcule a borda, ou o comprimento da circunferência e integre.C(r) = 2πr = 2π.√x = C(x)
Então:
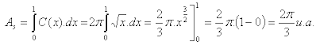






Soma de Riman! Lol!
ResponderExcluiropa, valeu...
ResponderExcluirjá corrigi.
Não era Riemann?
ResponderExcluir^^
Pow Favor Poderia colocar resoluçoes de calculo de volume (toro) fazendo com integral como achar esse volume!
ResponderExcluiraguardo...
agradeço