Método do Castilho: Resolvendo Sistema Qualquer

Um professor brasileiro, Castilho, preocupou-se em buscar um método para resolver os mais diversos tipos de sistemas, de forma genérica, e o mais simples possível. E conseguiu desenvolver um.

Primeiro, apenas para ilustrar o método, vamos usar um sistema de 2 equações com 3 variáveis (x, y, z); por tanto, as demais letras são constantes.

I) ax + by + cz = d
II) ex + fy + gz = h

O primeiro passo, é buscar sumir com uma variável, no caso x. Isso faremos uma espécie de mínimo divisor comum entre as duas equações. E apenas, para fins didáticos, considerarei (-ex) e (+ ax), mas não há problema algum em inverter os sinais.

I) ax + by + cz = d .(-ex)
II) ex + fy + gz = h .(+ax)

I) -aex² - bexy - cexz = - dex
II) aex² + afxy + agxz = ahx

Agora, somamos os dois sistemas, satisfazendo a igualdade aex².

(aex² - aex²) + (afxy – bexy) + (agxz – cexz) = (ahx – dex)

Resolvendo:

0 + afxy – bexy + agxz – cexz = ahx – dex

Perceba que a variável x é comum a todos os fatores. Então, denominaremos x um denominador comum a todos, de modo a poder simplificar o sistema, extinguindo a variável x.

x(afy – bey + agz – cez) = x(ah – de)

então

afy – bey + agz – cez = ah – de

Agora, podem colocar as variáveis em evidência.

(af – be)y + (ag – ce)z = (ah – de)

Aqui, foi um dos momentos mais surpreendentes. Castilho, percebeu que as constantes entre parênteses é o determinante de uma matriz 2x2.

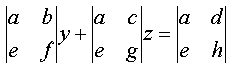
Percenbendo-se, que deste modo se obtem uma nova equação:

my + nz = q

Sendo que as constantes, m, n e q são os determinantes de uma matriz 2x2 das constantes originais.

Analisando bem o método. É meio intuitivo perceber, que ele pode ser repetido. Caso o sistema tivesse 3 equações, ter-se-ia duas equações de duas variáveis (y, z), de modo que repetindo o caso, ter-se-ia apenas uma equação com a variável z; o que facilmente se encontra o valor de z, e depois por substituição encontra-se as demais variáveis. E não importa quantas sejam as variáveis ou o tamanho do sistema, você sempre estará reduzindo as variáveis e apenas terá que trabalhar com o determinante de uma matriz 2x2 que é super simples. Sinceramente, creio que esse método é mil vezes melhor do que o famoso método de Crammer.

Vejamos agora um exemplo, para entender como funciona o método, desenvolvido por Castilho, na prática:

Sistema:
I) x + y + z = 9
II) x + 2y + z = 11
III) 2x – y – z = 0

(é um sistema que dá até para resolver de cabeça, mas apenas busca ilustrar o método).

Castilho transformou o método numa tabela, no qual se joga os dadas do sistema e do método:

Cada linha corresponde as equações (I, II e III). As colunas x, y, z, correspondes aos algarismo contidos nelas. TI refere-se ao valor da constante da igualdade de variável n0. E CC corresponde a soma dos valores da linha. Contudo, um grande mistério fica-se em torno de CC, pois não sei sua utilidade.
Agora, é só formar uma nova tabela, usando-se dos determinantes da matriz 2x2.

Portanto, tem-se:

-3z = - 12
Então, z = 4

Na primeira equação de 2 variáveis, já temos que: y = 2.

Numa equação de 3 variáveis, temos então:

x + y + z = 9
x + 2 + 4 = 9
x = 9 – 6
x = 3

Portanto: S = (3, 2, 4)

....

Esse método é super interessante pois nos faz lembrar um pouco do Brio Ruffini para resolver polinômios. É simples por apenas tratar de determinantes matrizes 2x2. A organização em colunas facilita a visualização e organização dos processos. E é simples e rápido, poucas passagens e contas; se for comparar com outros métodos para o mesmo.

Pensando algoritmicamente, é muito útil para engenheiros que tem que trabalhar muitas vezes com um sistema enorme, de muitas equações e varias variáveis. De modo que podem escrever um algoritmo num programa em C, Java etc. Que faça tais contas, de modo que até mesmo facilitará para o programa fazer a conta mais rápido; o que em grandes escalas pode fazer a diferença.

Contudo, é importante notar que o exemplo, trata-se de um sistema possível e determinado (SPD), no caso de indeterminado (SPI), ter-se-á valores zeros muitos determinantes. E caso for SI, impossível, certamente haverá alguns absurdos nos números. E pelo que pude verificar, tal método é apenas confiável para sistemas lineares.

E o enigma continua: Qual a finalidade de CC?